Hola!, en el día de hoy aprenderemos a optimizar nuestros problemas diarios gracias a una herramienta de Excel llamada “Solver”. Se fundamenta en un forma de razonar conocida como Problema de Programación Matemática (PPM) que abordaremos a continuación. A si es que ya sabes, si puedes ponerle números a tu problema (chicas lo siento, dramas del corazón aún no), Como Lo Hago te ayuda a resolverlos.
Más información después del salto.
Nota: El siguiente tutorial presenta cierto nivel de dificultad para usuarios no avanzados en Excel.
Comenzaremos definiendo algunos términos:
Lamentablemente la única forma de enseñarte a utilizar binarias en Solver es a través de un ejemplo en particular, de todas formas cualquier consulta o problema recuerda hacerlo a continuación de este artículo.
Partiremos viendo el ejemplo a resolver, obtenido de los ejercicios tipo del curso de Optimización de la Escuela de Agronomía e Ingeniería Forestal, Departamento de Economía Agraria de la Pontificia Universidad Católica de Chile:
Ejemplo:
Un parque tiene la siguiente distribución de lugares:

Distribución de lugares
Donde los números son las distancias en KM, O corresponde al origen y T al término o salida, las demás letras representan lugares interesantes que visitar como: “la laguna de los cisnes”, “el mirador”, “la zona de picnic”, entre otros. El guardaparques tiene su cabina en O y al término de la jornada de trabajo desea desplazarse a T en el menor tiempo posible, para lo cual debe escoger la ruta más corta.
Solución:
1.- Abrimos Excel y en una hoja nueva, dentro de las celdas, escribimos los parámetros, las variables de decisión, las restricciones y la función objetivo de manera ordenada:
Después de todo esto, deberiamos tener algo similar a lo siguiente:
Datos. Click para agrandar
2.- Comenzaremos a escribir las restricciones:
Nota: Los siguientes pasos se hacen tomando en consideración la posición respectiva de las celdas de la imagen superior. Para cualquier caso modifiquen las posiciones a las que hayan utilizado Uds.
En la celda I7 debemos decirle a Excel que O corresponde a un nodo de Origen, o sea, la suma de todos los arcos que empiezan con O menos los que terminan con O debe ser igual a 1. El número 1 se anota en la celda de al lado. Entonces en la celda I7 escribimos=suma(G7:G9)-suma(0). Debes notar que le estamos señalando las celdas que aún permanecen en blanco de la variable de decisión y no la de los parámetros. No te preocupes, Solver lo entenderá cuando se lo indiquemos.
En la celda I8 debemos decirle a Excel que A es nodo de paso, osea la suma de de los arcos que empiezan con A menos los que terminan con A debe ser 0. El número 0 se anota en la celda de al lado. Entonces en la celda I8 escribimos =suma(G11:G12)-suma(G7).
Debes realizar el mismo procedimiento con cada nodo que falta: B, C, D, E. Recordando colocar =suma(celdas de arcos que empiezan con la letra correspondiente)-suma(celdas de arcos que terminan con la letra correspondiente). Cuando llegues a T deberás anotar =suma(0)-suma(G24;G21).
Luego de eso se obtendrá una columna de restricciones repleta de ceros, como esta:
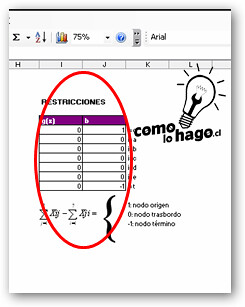
3.- Siguiendo con la función objetivo:
En la celda destinada a la función objetivo debemos indicarle al programa que debe buscar la suma producto de las celdas que empiezan con la misma letra, vale decir, debemos escribir=sumaproducto(celdas de parámetros que empiezan con O; celdas de variable de decisión que empiezan con O)+sumaproducto(celdas de parámetros que empiezan con A; celdas de variables de decisión que empiezan con A)+…+(celdas de parámetros que empiezan con E; celdas de variables de decisión que empiezan con E), así:

Definiendo función objetivo
Debes notar que no todos los nodos de los parámetros fueron colocados en la variable de decisión, a fin de que Solverpueda entender que no deseamos devolvernos en nuestra ruta, de esta forma, por ejemplo el arco DA no fue colocado en la variable de decisión puesto que si el guardaparque ya se encuentra en D, no queremos que se devuelva a A, sabemos que ese arco (DA) no estará aportando a la ruta más corta.
Una vez que tenemos definidas nuestras restricciones y nuestra función objetivo pasamos (¡¡¡al fin!!) a:
4.- Ejecutar Solver (Herramientas > Solver), con lo cual aparecerá la siguiente pantalla:
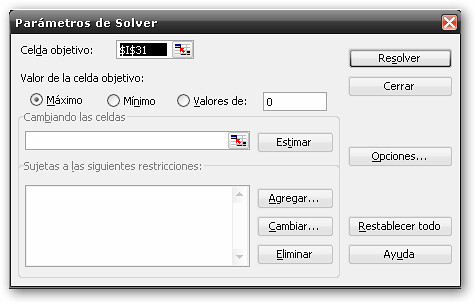
Solver
Llenaremos:
Click para ampliar
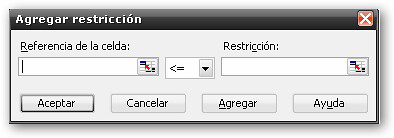
En “referencia de celda” debes incluir la columna con las restricciones de nodos. Para este caso de I7 a I13. En el espacio donde salen los signos <= debes buscar con la flechita y seleccionar = (estrictamente igual). En “Restricción” debes seleccionar la columna continua a la de las restricciones, para este caso desde J7 a J13. Luego pincha “Agregar”.
Ahora agregaremos la restricción de binaria, para esto en “referencia de celda” seleccionas las primeras tres celdas de la variable de decisión que se refieren a los arcos que puede formar O, esto es, las celdas desde G7 a G9. En el espacio que aparecen los signos <= debes buscar y seleccionar el que dice “bin” y observarás que automáticamente en el espacio de “restricción” aparece la palabra “binario”. Haz clic en “Agregar”. Agrega todas las binarias necesarias hasta terminar con las últimas celdas correspondientes a los nodos que se pueden formar con E. Obtendrás algo así:

Con esto ya le dijiste al programa todo lo que necesita saber para entregar el camino más corto.
5.- A continuación, presionamos “Resolver” y aparecerá la siguiente ventana:

Presiona “Aceptar”. En las celdas de la variable de decisión aparecerán “unos”(1’s) en aquellos arcos que el guardaparque deberá tomar a fin de recorrer el camino más corto. Veamos:
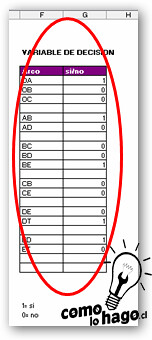
Luego, el camino más corto está dado por: O-A-B-E-D-T.
La distancia total recorrida puedes observarla en la celda de función objetivo. Y son 13 kilómetros.
Con esto has terminado tu PPM de ruta mínima y has minimizado la función que le permite al guardaparque llegar más rápido a su destino. ¡Felicidades! =). Es hora de que trates de resolver tus propios problemas. Estaremos aquí parta ayudarte. Suerte.
Cualquier duda o problema, pueden dejar un comentario en el área a continuación. Como siempre, este tutorial cuenta con el sello de garantía de Comolohago.cl
7:35:39 pm
hey!..el proximo semestre tendré que utilizar este manual!…que gran ayuda!..a ver si en un rato de ¿ocio? adelanto algo de trabajo!..jeje
muy buen aporte!
11:07:48 pm
sorry tengo una pregunta si me dan una tabla de notas y me dicen crear una formula q promedie las 2 notas mas altas de 3 es decir crer una formula q pueda identificar las mas altas
11:29:01 pm
@jossel: Te recomiendo revisar este tutorial donde se cubren esos aspectos de Excel:
http://www.comolohago.cl/2008/06/como-dominar-excel-parte-1/
Saludos
2:56:38 pm
hola como estas espero que bien ahhhhhhhhhhhh
me enseñaron demasiado gracias
6:06:00 pm
esta muy buena laq informasion y muy completo .bay
4:42:59 am
Muchas gracias por la información¡ me ayudó mucho para hacer una tarea. Muy bien explicado.
Gracias
2:51:45 am
viejo revise el tutorial, y necesitaba resolver este problema, pero con arcos dirigidos. lo modele con gams y el resultado es perfecto un Z= 55, pero al resolverlo con solver me da 150. no se qeu hize mal.
9:44:25 am
Excelente explicación… Muchas felicidades y muchas gracias!!!
9:49:27 pm
mmmm iba bien hasta que lo resolví xD y no me tomó en cuenta los nodos de termino !!! ayuda por favor!
11:22:15 am
facil la wea…. peka!